○千水湖で採水しました。

○採取された植物プランクトンは、主に3種類でした。

○水質と、植物プランクトンの総細胞体積は、似た形を示していました。

○競合がないと仮定した場合の計算ですが、あまりうまくいきませんでした。

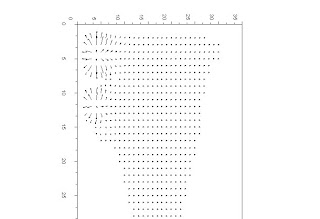
○競合があると仮定した場合のScilabによる計算結果(種の変遷の様子が計算されました)。

より長期間を仮定して計算すると、どうなるのか。
Scilabで、計算時間を延長(8年間分)した場合。
初期値による、結果の「鋭敏性」のようなものがみられました。
(なお、3種類の相互作用について、天体の「3体問題」や、気象の「ローレンツ・アトラクタ」(3変数)では、初期値の僅かな変化で結果が大きく異なってしまうことが示されています。)



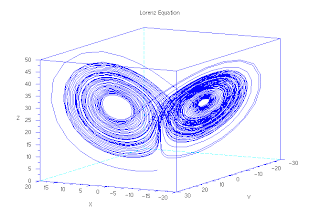 Scilabでの計算例
Scilabでの計算例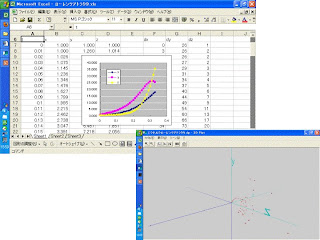
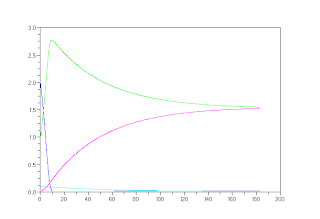 青 :リン
青 :リン